Cracking the Secret Code of 4-Cushion Billiards
For most people, billiards is a game of skill, patience, and practice. But when you enter the world of carom billiards, particularly the four-cushion system, you discover an entirely different dimension of the sport—one that blends geometry, mathematics, and physics into every shot.
The diagrams you see above are not just abstract lines and numbers. They represent a mathematical framework that professional players use to calculate complex rebound shots. With the right formulas, what looks impossible to a casual player suddenly becomes predictable and achievable. Let’s dive into how this fascinating system works.

The Basics of Four-Cushion Billiards
Unlike pool, where the goal is to pocket balls, carom billiards (and especially the four-cushion variation) requires the cue ball to hit at least four cushions before contacting the target ball. This makes the game a test of precision and foresight.
To succeed, players rely on a numeric “diamond system” marked on the rails of the table. These reference points allow them to apply mathematical formulas to determine the path of the cue ball.
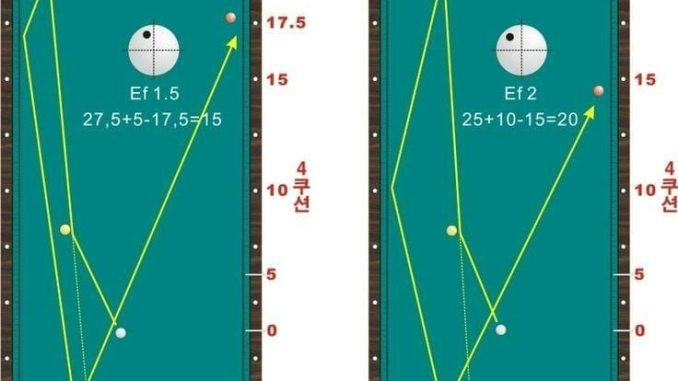
In the diagrams, you can see numbers such as 27.5, 5, 17.5, 25, 10, and 15. These are not random—they correspond to calculated positions on the rails that ensure the cue ball travels exactly where the player wants.
Understanding the Formula
Take the first diagram (left side). The formula is:
27.5 + 5 – 17.5 = 15
This calculation predicts the destination point of the cue ball after it rebounds across four cushions. Each number represents a starting point, an angle of entry, and adjustments for rebounds.
On the second diagram (right side), the formula changes:
25 + 10 – 15 = 20
Here again, by applying simple addition and subtraction, the player determines the correct line for the cue ball to strike the final target.
This numeric system transforms a seemingly chaotic sequence of rebounds into a predictable and repeatable outcome.
Why the System Works
The success of the four-cushion system comes down to physics and geometry:
-
Law of Reflection: When the cue ball strikes a cushion, the angle of incidence equals the angle of reflection.
-
Consistent Measurements: By using diamonds (the small markers on the rails) as reference points, players can apply equations to calculate angles.
-
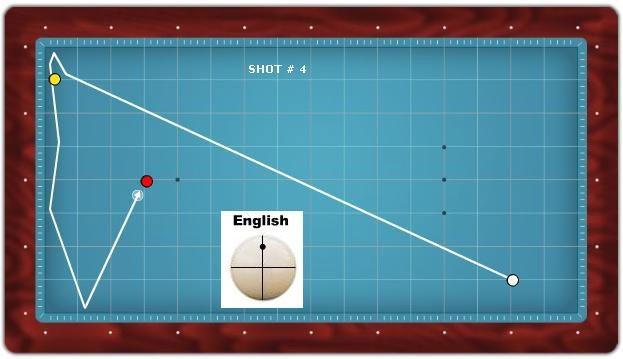
Adjustments for Spin: While math provides the base path, adding spin (English) fine-tunes the cue ball’s movement.
Together, these principles ensure that what looks like a miracle shot is actually the result of careful calculation.

The Role of Ef (Effect Factor)
In both diagrams, you see terms like Ef 1.5 and Ef 2. This represents the effect factor, which accounts for spin, speed, and table conditions.
-
Ef 1.5 means a lighter stroke with moderate spin.
-
Ef 2 indicates stronger spin and speed.
By adjusting the effect factor, players can adapt the same formula to different table conditions or shot requirements.
Step-by-Step Example
Let’s break down a practical application using the second diagram:
-
Start point: Cue ball position marked as 25.
-
Add adjustment: +10 to account for the entry angle.
-
Subtract cushion impact: –15.
-
Final target point = 20.
This tells the player exactly where the cue ball will end up after four cushions. Instead of relying on guesswork, the formula delivers a precise prediction.

Advantages of the Four-Cushion System
-
Accuracy – Once you understand the formula, you can consistently repeat shots.
-
Confidence – Instead of fearing “lucky” rebounds, you know where the ball is going.
-
Strategy – Advanced players plan several shots ahead using this method.
-
Universal Application – The system works across different tables and conditions, as long as adjustments are made for spin and speed.
Common Mistakes Beginners Make
Even with the formula, many beginners struggle at first. The most common mistakes include:
-
Ignoring Spin: The math works only if you control side spin properly. Too much or too little alters the outcome.
-
Overhitting the Cue Ball: Power is less important than precision. Excessive speed changes rebound angles.
-
Not Adjusting for Table Conditions: Old or new cloth, cushion elasticity, and humidity all affect the path.
That’s why professional players don’t just rely on numbers—they combine them with years of experience.
The Beauty of Math in Billiards
What makes the four-cushion system so fascinating is how it merges two worlds:
-
Artistry: Choosing creative rebound paths to reach the target ball.
-
Science: Using formulas to guarantee accuracy.
This blend transforms billiards from a casual game into a mental sport where players are not only athletes but also problem-solvers. Watching a master execute these shots feels like seeing a magician at work—but the “magic” is really math.
How to Practice the System
If you want to apply this method to your own game, here are some steps:
-
Learn the Diamond System: Familiarize yourself with the numeric values on the rails.
-
Start Simple: Practice with two- or three-cushion shots before moving to four.
-
Experiment with Spin: Notice how changing Ef values alters the outcome.
-
Record Your Shots: Keep track of successful formulas for future use.
With time, the calculations become automatic. Instead of manually adding and subtracting, you’ll develop an instinctive feel for the numbers.

Conclusion
The diagrams we began with are not just mathematical curiosities. They represent a powerful system that unlocks the hidden science of billiards. By applying the four-cushion formula, players can achieve accuracy that looks impossible to the untrained eye.
Next time you watch a skilled player making complex rebound shots, remember: behind the artistry is a precise equation guiding the cue ball across the table.
Billiards is more than a game of chance—it’s a game of numbers, angles, and the elegant dance of mathematics on green felt.